回路-24-2

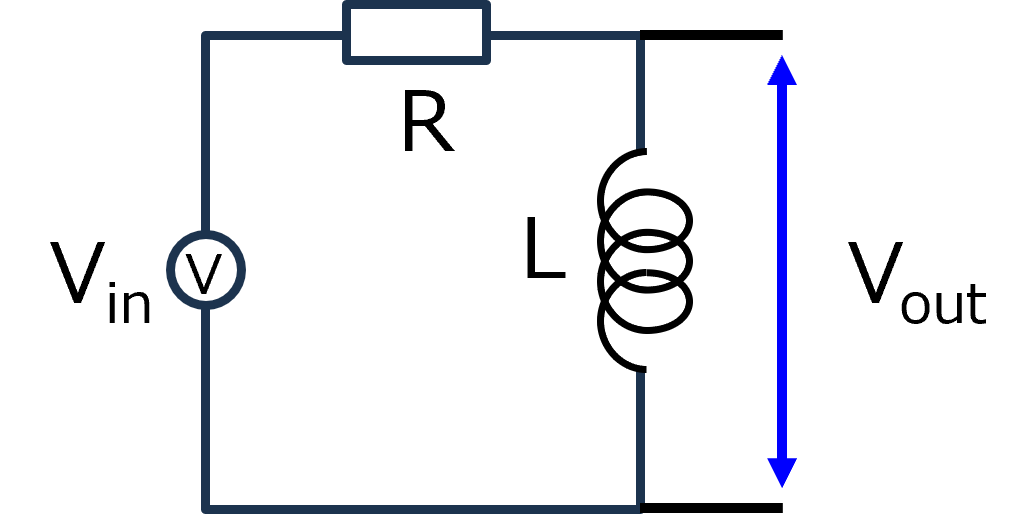
RLハイパスフィルタを電流から考える

せっかく，RL直列回路での電流を計算したので，電流から，各素子間の電圧を求めていきましょう．

今回は，定常状態について考えていきます．

したがって，

　過渡項は考えない

　積分は不定積分

として計算します．

・基本関係式

\(\Large \displaystyle V_C(t) = \frac{1}{ C} \int I(t) \ dt \)　

\(\Large \displaystyle V_L(t) = L \ \frac{d}{ dt} I(t) \)　

\(\Large \displaystyle V_R(t) = R \cdot I(t) \)　

RL直列回路においては，定常状態での電流は，

\(\Large \displaystyle I(t) = \frac{V_0 \ e^{ -j \theta}}{ \sqrt{R^2 +( \omega L)^2}} \cdot e^{j \omega t} \)　

\(\Large tan \ (- \theta) = \displaystyle \frac {\omega L }{R}\)　

もしくは，

\(\Large \displaystyle I(t) = \frac{V_0 \ e^{ j \theta}}{ \sqrt{R^2 +( \omega L)^2}} \cdot e^{j \omega t} \)　

\(\Large tan \ ( \theta) = \displaystyle - \frac {\omega L }{R}\)　

となります．

・L

\(\Large \displaystyle V_L(t) = L \frac{d}{dt} \frac{V_0 \ e^{ j \theta}}{ \sqrt{R^2 +( \omega L)^2}} \cdot e^{j \omega t} \)　

\(\Large \displaystyle =\frac{V_0 \ e^{ j \theta}}{ \sqrt{R^2 +( \omega L)^2}} \cdot j \omega \cdot e^{j \omega t} \)　

ここで，

\(\Large \displaystyle e^{ j \theta} = cos \ \theta + j \ sin \ \theta \)　

\(\Large \displaystyle e^{ j \frac{\pi}{2}} = cos \ \frac{\pi}{2} + j \ sin \ \frac{\pi}{2} = j \)　

より，

\(\Large \displaystyle V_L(t) =V_0 \frac{\omega L }{ \sqrt{R^2 +( \omega L)^2}} \cdot e^{ j \theta} \cdot j \cdot e^{j \omega t} \)　

\(\Large \displaystyle =V_0 \frac{\omega L }{ \sqrt{R^2 +( \omega L)^2}} \cdot e^{ j \theta} \cdot e^{ j \frac{\pi}{2}} \cdot e^{j \omega t} \)　

\(\Large \displaystyle =V_0 \frac{\omega L }{ \sqrt{R^2 +( \omega L)^2}} \cdot e^{j (\omega t + \theta +\frac{\pi}{2})} \)　

ここで，

\(\Large \theta = \displaystyle tan^{-1} \left(-\frac {\omega L }{R} \right)\)　

となるので，

\(\Large \displaystyle V_C(t) = \frac{V_0 \ e^{ j \theta}}{ \sqrt{(\omega RC)^2 + 1}} \cdot \ e^{j (\omega t - \varphi) } \)　

\(\Large \varphi = - tan^{-1} (\omega RC)\)　

となり，ここ，で計算したローパスフィルタと一致します．