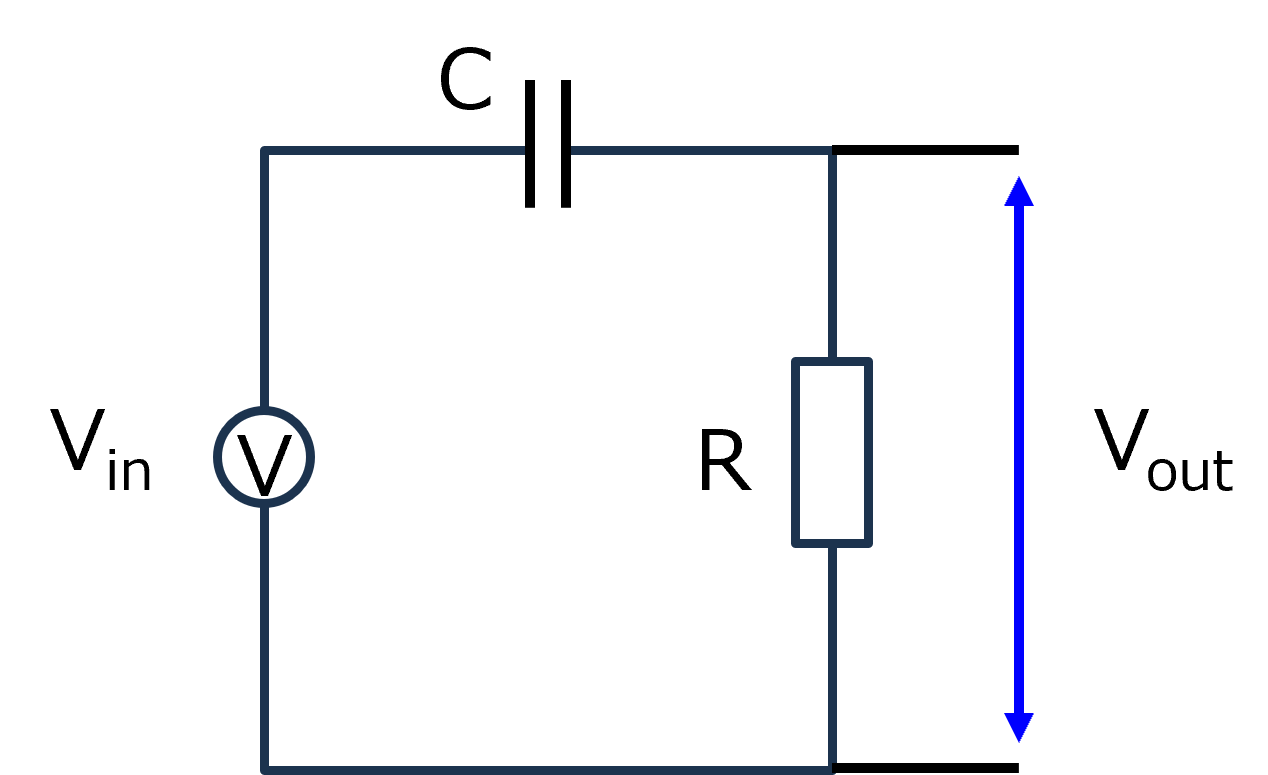
回路-22

RCハイパスフィルタ

次は，ハイパスフィルタ

よく，教科書などで使われる図は，

先程のローパスフィルタは，コンデンサ部の電圧でしたが，ハイパスフィルタの場合は，抵抗部の電圧となります．

・インピーダンス

一番定番の，インピーダンス，から求めていきます．

インピーダンスなので，定常状態，での特性を見ることになります．スイッチオンでの過渡現象は見ません．

これが一番わかりやすい方法だと思います．

全体のインピーダンスは，

\(\Large Z = \displaystyle R + \frac{1}{j \omega C} \)　

となります．抵抗部の電圧，V_out，のインピーダンスは，

\(\Large Z_{out} = \displaystyle R \)　

となるので，伝達関数，は，

\(\Large G( j \omega) = \displaystyle \frac{V_{out}}{V_{in}} = \frac{Z_{out} \cdot I}{Z \cdot I} = \frac {Z_{out}}{Z} = \frac{ R}{R + \frac{1}{j \omega C}} \)　

\(\Large \displaystyle = \frac{ j \omega R C}{1 + j \omega R C} = \frac{ j \omega R C(1 - j \omega R C)} {1 + ( \omega R C)^2 }= \frac{ ( \omega R C)^2 + j \omega R C} {1 + ( \omega R C)^2 } \)　

となります．利得は，複素数の絶対値を考えればいいです．

複素数の絶対値は，

\(\Large z = a + b \ i\)　

\(\Large |z| =\sqrt{ a^2 + b^2} \)　

となるので，

\(\Large G( j \omega) = \displaystyle \frac{( \omega R C)^2 + j \omega R C} {1 + ( \omega R C)^2 } = \frac{ \omega R C} {1 + ( \omega R C)^2 } ( \omega R C + j)\)　

\(\Large | G( j \omega)| = \displaystyle \frac{ \omega R C} {1 + ( \omega R C)^2 } \cdot \sqrt{(\omega R C)^2 +1} = \frac{ \omega R C} { \sqrt{1 + (\omega R C)^2 }}\)　

となります．

\(\Large \omega \sim 0 \ : \ | G( j \omega)| = 0 \)　

\(\Large \omega \sim \infty \ : \ | G( j \omega)| = 1 \)　

となり，ハイパスフィルタ，となります．

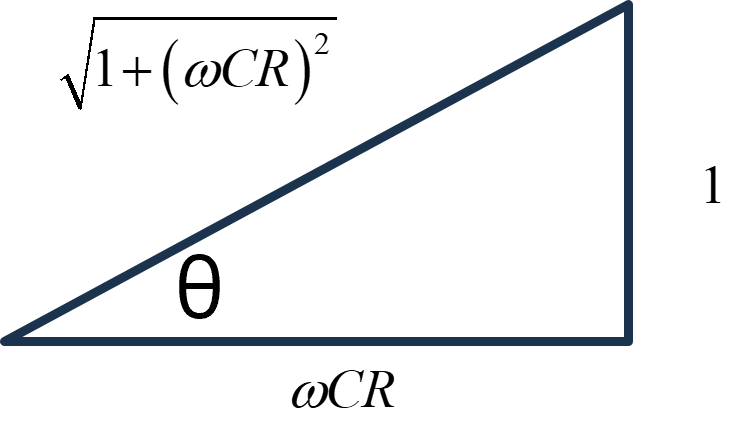
位相角は，複素項／実数項，となりますので，

\(\Large tan \ \theta = \displaystyle \frac{1}{\omega R C } \)　

\(\Large \theta = \displaystyle tan^{-1} \frac{1}{\omega R C } \)　

となります．

実際に，LTspice，とエクセルでの計算結果を確認すると，

R　：　10 Hz
C　：　0.1 F

において，

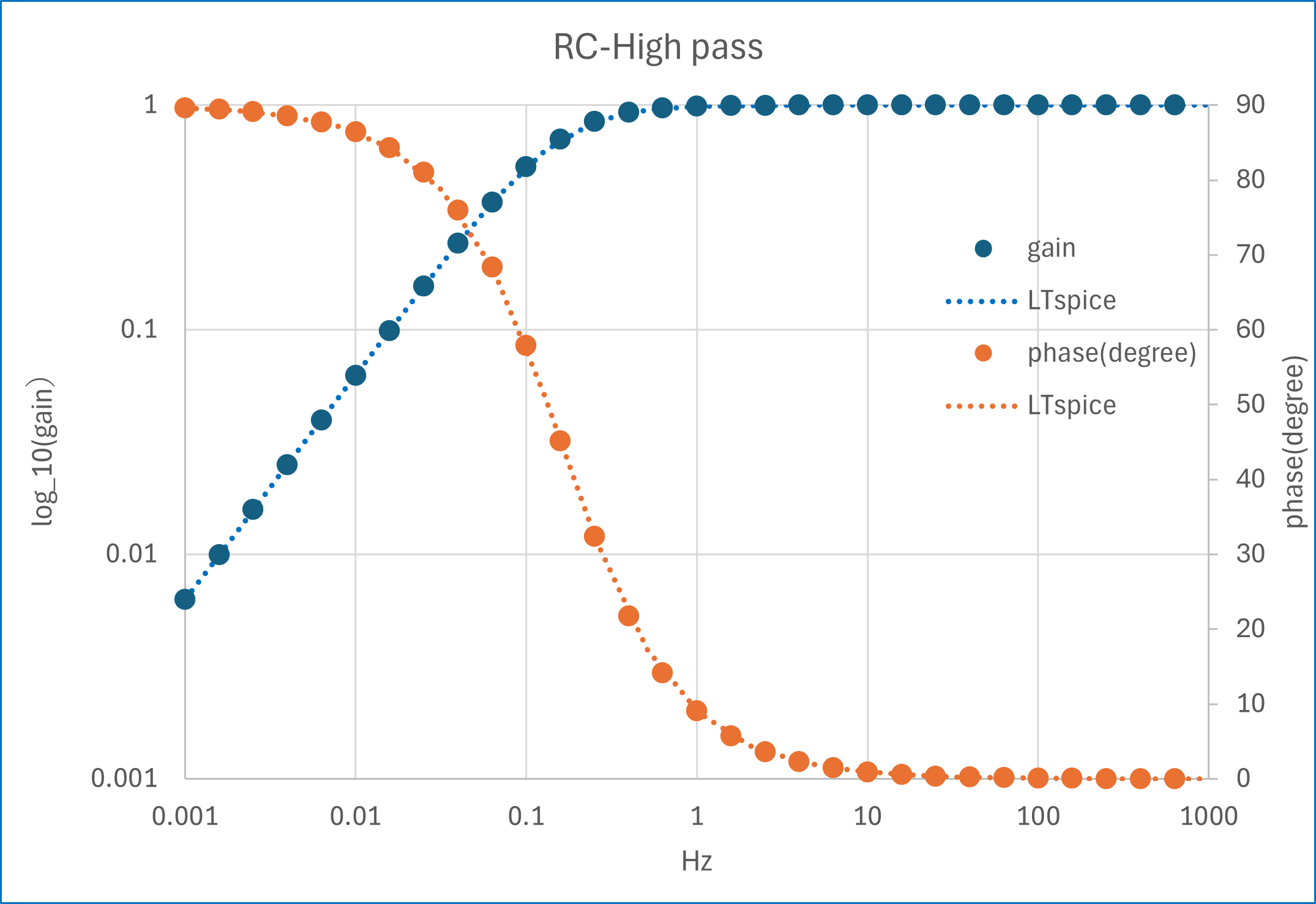
と一致することがわかります．

せっかくなので，ここ，に過渡現象を含めたRLの並列直列交流回路にを計算していきます．