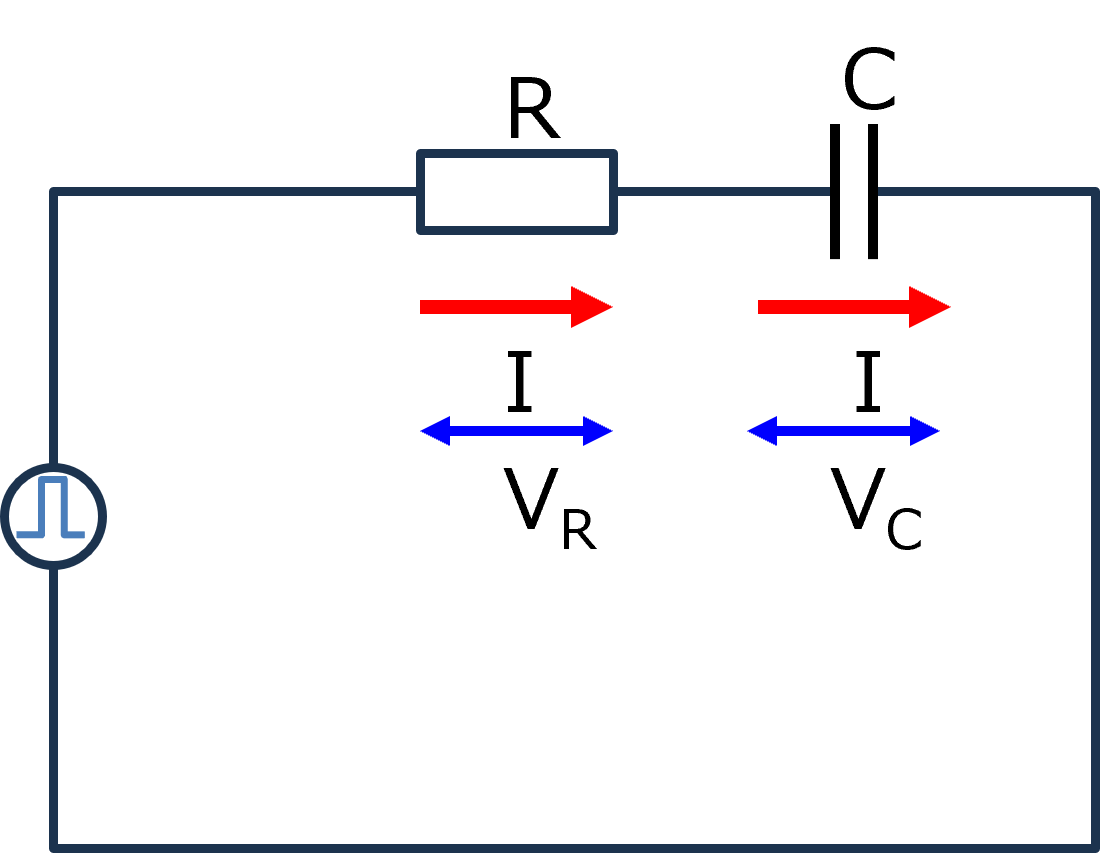
14-1-2.ステップ関数(RC回路)
このページからは,入力が正弦波ではなくステップ関数の場合の応答を,q,から調べていきます.
次は,抵抗,コンデンサが直列の回路について

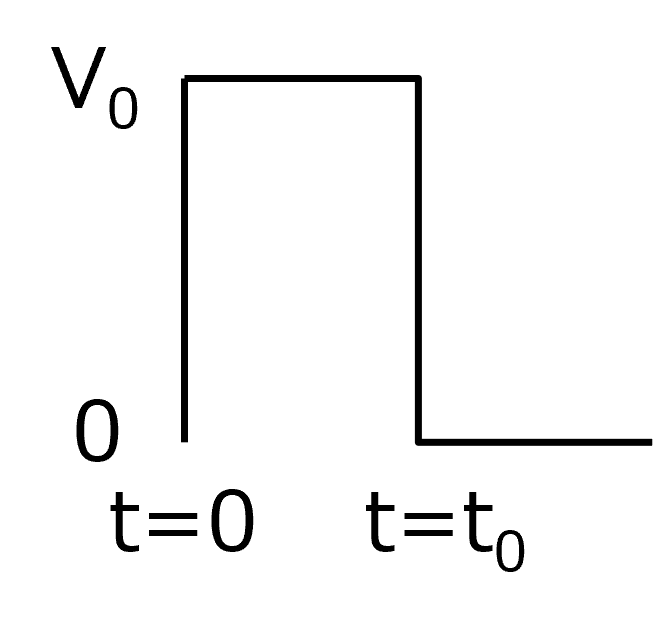
入力はステップ関数となるので,
\(\Large V(t) \ : \ V_0 \ ( 0 \leq t \leq t_0) \)
\(\Large \hspace{35 pt} : \ 0 \ (t_0 < t) \)
となります.
直列なので,
電流はどこも同じ
電圧は,抵抗+コンデンサ,が電源と等しい
ことから,
\(\Large V_0 = V_R (t) + V_C (t) \)
\(\Large V_R = R \cdot I(t) \)
\(\Large \displaystyle I(t) = C \ \frac{d}{dt} V_C (t) \)
と,ここまでは同じですが,
\(\Large \displaystyle I(t) = \ \frac{d \ q(t)}{dt} \)
となるので,
\(\Large \displaystyle V_R = R \cdot I(t) = R \ \frac{d \ q(t)}{dt} \)
\(\Large \displaystyle V_C(t) = \frac{1}{C} \ \int \ I (t) \ dt = \frac{1}{C} \ q(t) \)
となります.したがって,
\(\Large \displaystyle V_0 = V_R (t) + V_C (t) = R \ \frac{d \ q(t)}{dt} + \frac{1}{C} \ q(t) \)
なる,微分方程式を解けばいいことになります.
\(\Large 0 \leq t \leq t_0 \)
\(\Large \displaystyle \frac{d}{dt} q (t) = - \frac{1}{R \cdot C} \ q (t) + \frac{1}{R } \ V_0 \)
定数変化法を使って,
\(\Large \displaystyle q(t) = A_0 \cdot exp \left( - \frac{1}{R \cdot C} \ t \right) \)
\(\Large \displaystyle \frac{d}{dt} q (t) = A_0' \cdot exp \left( - \frac{1}{R \cdot C} \ t \right) \color{blue}{- \frac{1}{R \cdot C} \cdot A_0 \cdot exp \left( - \frac{1}{R \cdot C} \ t \right)} = \color{blue}{- \frac{1}{R \cdot C} V_C (t)} + \frac{1}{R } \ V_0 \)
\(\Large \displaystyle A_0' \cdot exp \left( - \frac{1}{R \cdot C} \ t \right) = \frac{1}{R} \ V_0 \)
\(\Large \displaystyle A_0' = \frac{1}{R} \ V_0 \cdot exp \left( \frac{1}{R \cdot C} \ t \right) \)
\(\Large \displaystyle A_0 = V_0 \cdot C \cdot exp \left( \frac{1}{R \cdot C} \ t \right) + D \)
\(\Large \displaystyle q(t) = \left\{ V_0 \cdot C \cdot exp \left( \frac{1}{R \cdot C} \ t \right) + D \right\} \cdot exp \left( - \frac{1}{R \cdot C} \ t \right) \)
\(\Large \displaystyle q(t) = V_0 \cdot C + D \cdot exp \left( - \frac{1}{R \cdot C} \ t \right) \)
t=0 : q(0) = 0,
\(\Large \displaystyle 0 = q(0) = V_0 \cdot C + D \)
\(\Large \displaystyle D = - V_0 \cdot C\)
\(\Large \displaystyle q(t) = V_0 \cdot C - V_0 \cdot C \cdot exp \left( - \frac{1}{R \cdot C} \ t \right) \)
\(\Large \displaystyle V_C(t) = V_0 \cdot C \left\{ 1- exp \left( - \frac{1}{R \cdot C} \ t \right) \right\} \)
\(\Large \displaystyle I(t) = \ \frac{d}{dt} q (t) = C \cdot V_0 \left( - \frac{1}{R \cdot C} \right) \left\{- exp \left( - \frac{1}{R \cdot C} \ t \right) \right\} = \frac{V_0}{R} exp \left( - \frac{1}{R \cdot C} \ t \right) \)
とVCで解いた結果と一致します.
ここで,
なぜ,q(0)=0,なのだろう
と気になったので,Copilot,に聞いてみると,
Copilotの返答
コンデンサは電荷を蓄える素子ですが、回路に電源が接続される前(つまり )には、電荷が蓄積されていないと仮定するのが一般的です。
これは以下のような理由によります:
・ステップ応答解析では、回路は で突然電源がオンになると仮定します。
・それ以前(t<0)は電源がオフで、コンデンサには電荷が蓄積されていない(=電圧ゼロ)とするのが自然です。
・コンデンサの電荷と電圧の関係は なので、電圧がゼロなら電荷もゼロ。
ということでした.
あとは同じなので,省略します.
次は,同様のRC回路を,電荷,q,から考えてみます.です.